[WriteUp] / [Cryptohack - Elliptic Curves, Efficient Exchange]
2025. 6. 17. 22:31ㆍHacking/암호학

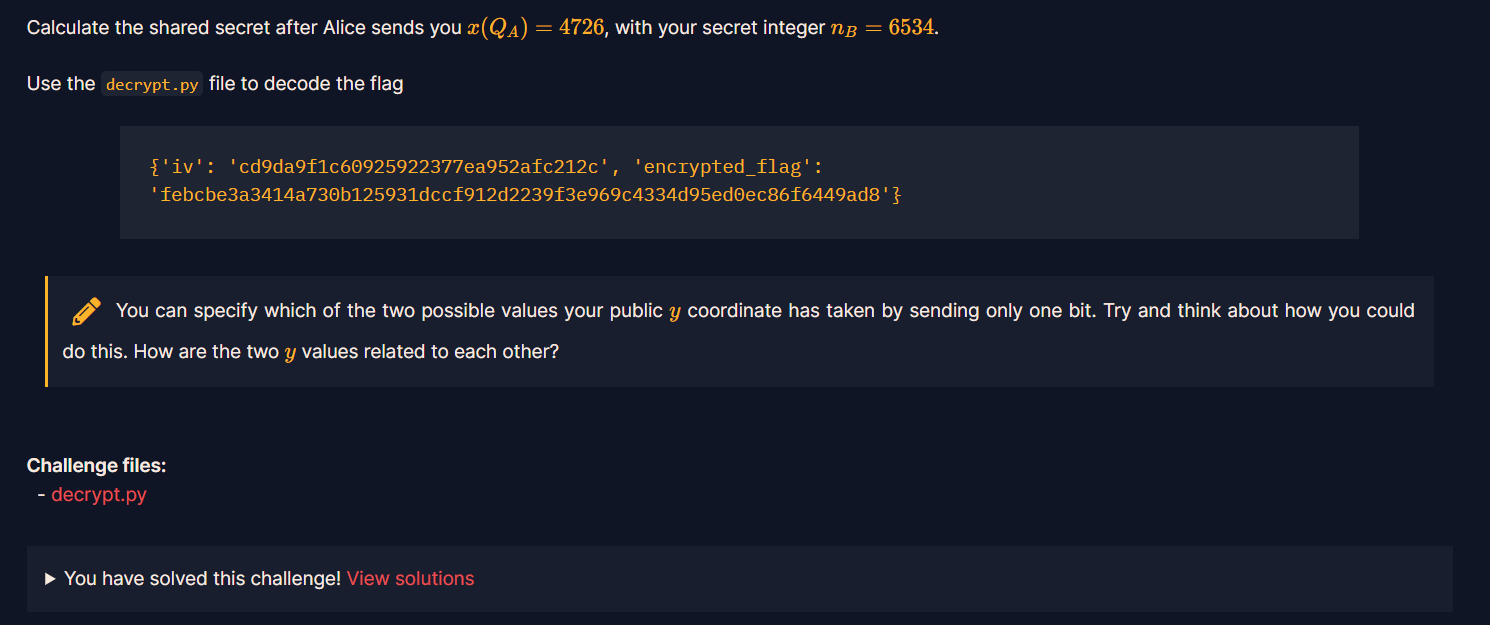
그리고
decrypt.py
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad, unpad
import hashlib
def is_pkcs7_padded(message):
padding = message[-message[-1]:]
return all(padding[i] == len(padding) for i in range(0, len(padding)))
def decrypt_flag(shared_secret: int, iv: str, ciphertext: str):
# Derive AES key from shared secret
sha1 = hashlib.sha1()
sha1.update(str(shared_secret).encode('ascii'))
key = sha1.digest()[:16]
# Decrypt flag
ciphertext = bytes.fromhex(ciphertext)
iv = bytes.fromhex(iv)
cipher = AES.new(key, AES.MODE_CBC, iv)
plaintext = cipher.decrypt(ciphertext)
if is_pkcs7_padded(plaintext):
return unpad(plaintext, 16).decode('ascii')
else:
return plaintext.decode('ascii')
shared_secret = ?
iv = ?
ciphertext = ?
print(decrypt_flag(shared_secret, iv, ciphertext))
-> exploit.py
# Given values
p = 9739
x_QA = 4726
nB = 6534
# Find possible y values for the given x using the curve equation:
# y^2 = x^3 + 497x + 1768 mod p
rhs = (x_QA**3 + 497 * x_QA + 1768) % p
# Find modular square roots of rhs (i.e., y such that y^2 = rhs mod p)
# Using Tonelli-Shanks algorithm to find sqrt mod p
from sympy.ntheory import sqrt_mod
y_candidates = sqrt_mod(rhs, p, all_roots=True)
# Compute shared secrets and try decrypting both
possible_flags = []
for y in y_candidates:
QA = (x_QA, y)
# ECC scalar multiplication
shared_secret = scalar_mult(nB, QA)
x_shared_secret = shared_secret[0]
# Derive AES key from x-coordinate
sha1 = hashlib.sha1()
sha1.update(str(x_shared_secret).encode('ascii'))
key = sha1.digest()[:16]
# Provided ciphertext and iv
ciphertext_hex = 'febcbe3a3414a730b125931dccf912d2239f3e969c4334d95ed0ec86f6449ad8'
iv_hex = 'cd9da9f1c60925922377ea952afc212c'
ciphertext = bytes.fromhex(ciphertext_hex)
iv = bytes.fromhex(iv_hex)
# Decrypt
cipher = AES.new(key, AES.MODE_CBC, iv)
plaintext = cipher.decrypt(ciphertext)
try:
flag = unpad(plaintext, 16).decode('utf-8')
except:
flag = plaintext.hex()
possible_flags.append((y, flag))
possible_flagsAlice와 Bob이 타원곡선 위에서 키 교환을 했고
- 우리는 Bob의 private key nB, Alice의 public key Q_A = (x_QA, y_QA) 중 x_QA만 받았음.
- 따라서 y_QA의 가능한 두 개의 값을 구한 뒤,
- 각 경우에 대해 공유 비밀 키를 계산하고
- 그 키를 AES-CBC 복호화에 사용해 플래그를 추출하는 코드.
crypto{3ff1c1ent_k3y_3xch4ng3}
'Hacking > 암호학' 카테고리의 다른 글
| [WriteUp] / [CryptoHack - Great Snakes] (0) | 2025.06.17 |
|---|---|
| [WriteUp] / [Cryptohack - Finding Flags] (0) | 2025.06.17 |
| [WriteUp] / [CryptoHack - Elliptic Curves, Curves and Logs] (0) | 2025.06.17 |
| [WriteUp] / [CryptoHack - Elliptic Curves, Scalar Multiplication] (0) | 2025.06.17 |
| [WriteUp] / [CryptoHack - Elliptic Curves, Point Addition] (0) | 2025.06.17 |